正态分布（钟形曲线）简介

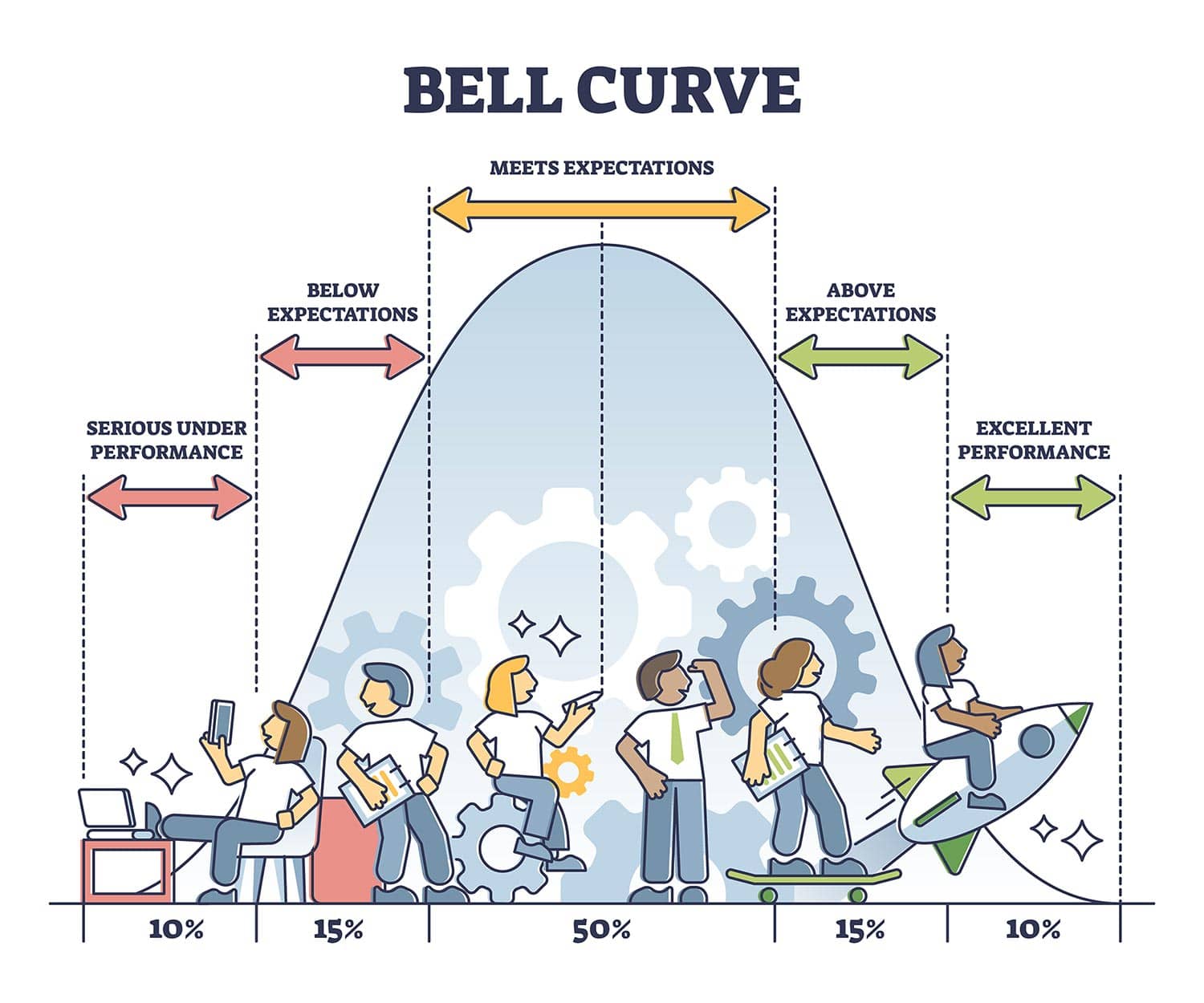
钟形曲线，也称为正态分布或高斯分布，是统计学中的一种对称概率分布。它表示一个图表，数据围绕均值聚集，在中心频率最高，并逐渐向两侧减少。

正态分布的性质

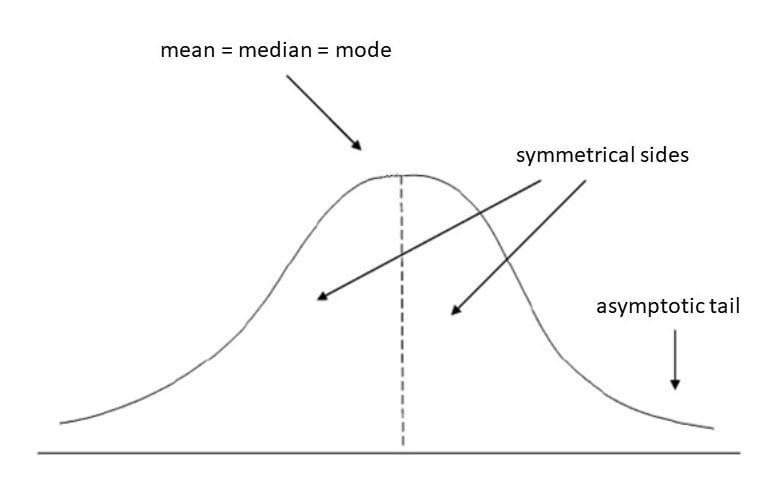
正态分布是一种连续概率分布，其在均值两侧是对称的，因此中心右侧是左侧的镜像。

正态分布曲线下的面积代表概率，整个曲线下面积之和为一。

大多数正态分布中的连续数据值倾向于围绕均值聚集，值离均值越远，出现的可能性就越小。尾部是渐近的，这意味着它们接近但永远不会触及水平线（即x轴）。

对于完美的正态分布，均值、中位数和众数将是相同的值，视觉上由曲线的峰值表示。

正态分布与标准正态分布

正态分布由两个参数决定：均值和方差。均值为0，标准差为1的正态分布称为标准正态分布。

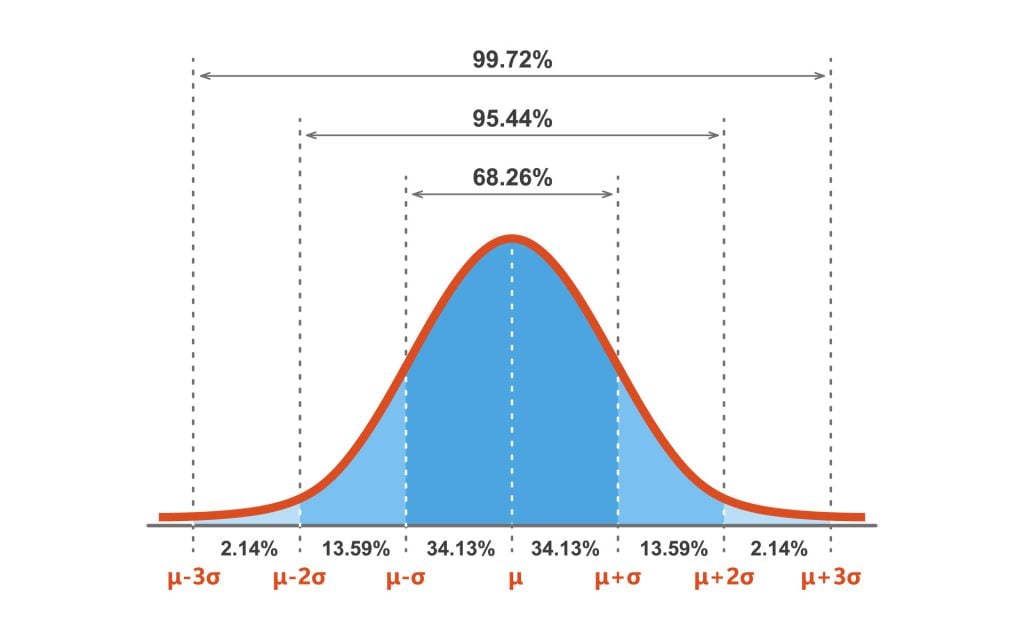
图1. 标准正态分布（SND）。

这是用于构建正态分布表的分布。

为什么正态分布很重要？

钟形曲线是自然和心理学中的常见特征

正态分布是统计学中最重要的概率分布，因为许多自然和心理学中的连续数据在编译和绘制时都会显示这种钟形曲线。

例如，如果我们随机抽取100名个体，我们期望看到许多连续变量的正态分布频率曲线，如智商、身高、体重和血压。

参数显著性检验需要样本数据点的正态分布

心理学家使用的最强大的（参数）统计检验要求数据呈正态分布。如果数据不呈钟形曲线，研究人员可能会使用一种称为非参数统计的较弱统计检验。

将正态分布的原始分数转换为z分数

我们可以通过将正态分布的值（原始分数）标准化为z分数来实现这一点。

此过程允许研究人员确定落在均值特定数量标准差范围内的值的比例（即计算经验法则）。

经验法则公式是什么？

统计学中的经验法则允许研究人员确定落在均值特定距离内的值的比例。经验法则通常被称为三西格玛法则或68-95-99.7法则。

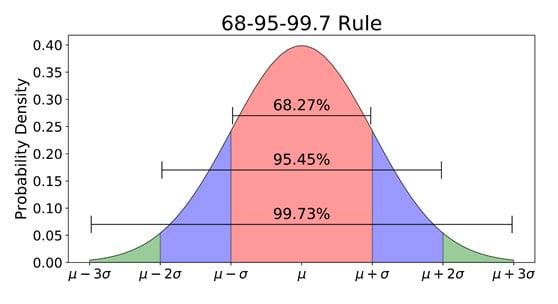
如果正态分布中的数据值被转换为标准分数（z分数），则经验法则描述了落在均值（μ）特定数量标准差（σ）范围内的数据百分比。

经验法则允许研究人员计算从正态分布中随机获得分数的概率。

68%的数据落在均值的第一个标准差范围内。这意味着有68%的概率随机选择一个分数，该分数在均值的-1到+1标准差之间。

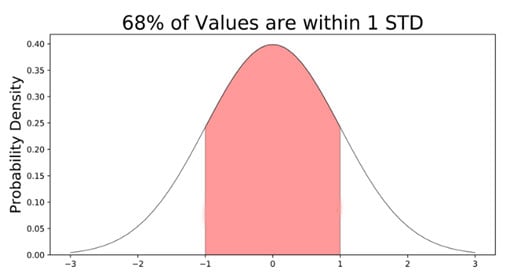
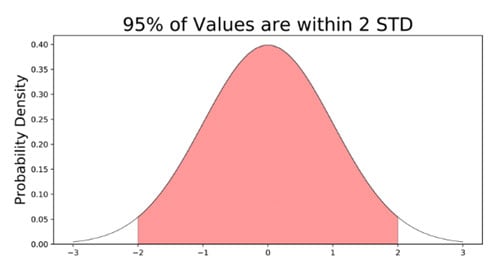
95%的值落在均值的两个标准差范围内。这意味着有95%的概率随机选择一个分数，该分数在均值的-2到+2标准差之间。

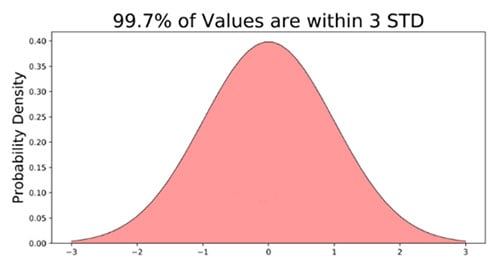
99.7%的数据将落在均值的三个标准差范围内。这意味着有99.7%的概率随机选择一个分数，该分数在均值的-3到+3标准差之间。

如何检查数据

统计软件（如SPSS）可用于通过计算集中趋势的三个度量来检查您的数据集是否呈正态分布。如果均值、中位数和众数非常相似，则有很大可能数据遵循钟形分布（SPSS命令在这里）。

建议同时使用频率图，以便您可以检查数据的视觉形状（如果您的图表是直方图，可以使用SPSS添加分布曲线：从菜单中选择：Elements > Show Distribution Curve）。

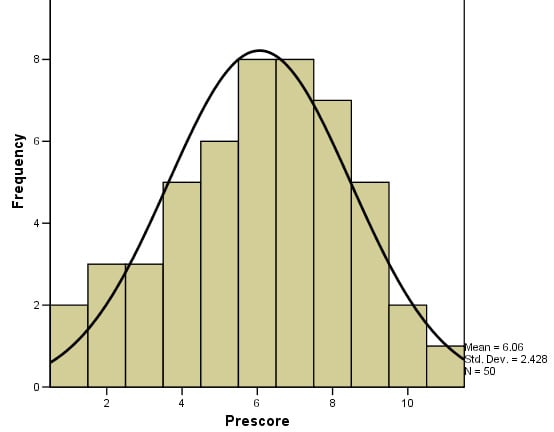
随着测量水平的细化和从总体中抽取的样本量的增大，正态分布变得更加明显（即完美）。

您还可以计算系数，这些系数告诉我们分布尾部相对于钟形曲线中间部分的大小。例如，可以使用SPSS计算Kolmogorov-Smirnov和Shapiro-Wilk检验。

这些检验将您的数据与正态分布进行比较，并提供一个p值，如果p值显著（p < .05），则表明您的数据与正态分布不同（在这种情况下，我们不希望得到显著结果，而需要一个高于0.05的p值）。

进一步信息

• 正态分布的深入定义（Kahn Academy）
• 标准正态分布和经验法则（Kahn Academy）
• 心理学统计书籍下载

  正态分布的峰度是0还是3？

正态分布的峰度为3。然而，有时人们使用“超峰度”，即从分布的峰度中减去3，以与正态分布进行比较。

在这种情况下，正态分布的超峰度将是 3 − 3 = 0。

因此，正态分布的峰度为3，但其超峰度为0。

引用来源

本文翻译自以下网站：

simplypsychology.org

使用声明

本文仅供教育和参考用途。如需转载或引用，请注明出处和作者。

如果你有任何问题或建议，请随时联系微信公众号。