置信区间解释:示例、公式与解读
什么是95%置信区间?
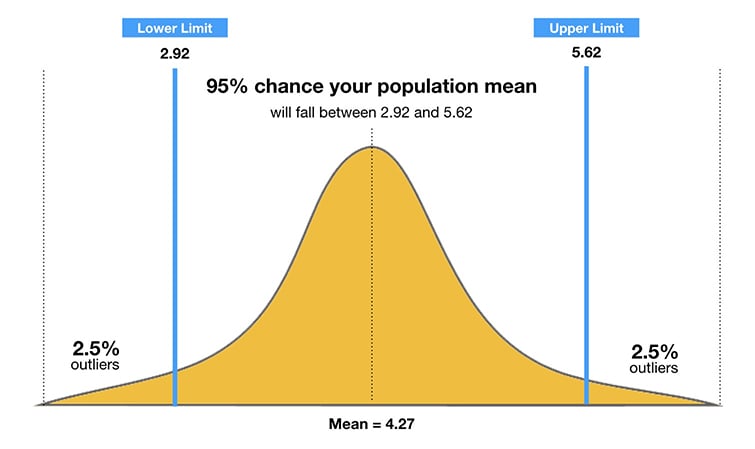
95%置信区间是一组值,你可以有95%的信心认为它包含了总体的真实均值。由于自然抽样变异性,样本均值(置信区间的中心)会因样本而异。
置信度在于方法,而不在于某个特定的置信区间。如果我们多次重复抽样方法,大约95%的构建区间将捕捉到总体的真实均值。
因此,随着样本量的增加,区间值的范围将变窄,这意味着你比小样本时更准确地知道均值。
我们可以使用正态分布来可视化这一点(见下图)。
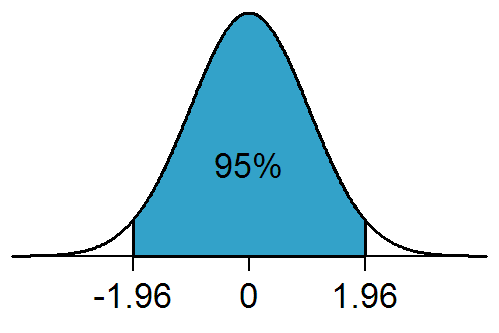
例如,总体均值在样本均值的-1.96和+1.96标准差(z分数)之间的概率为95%。
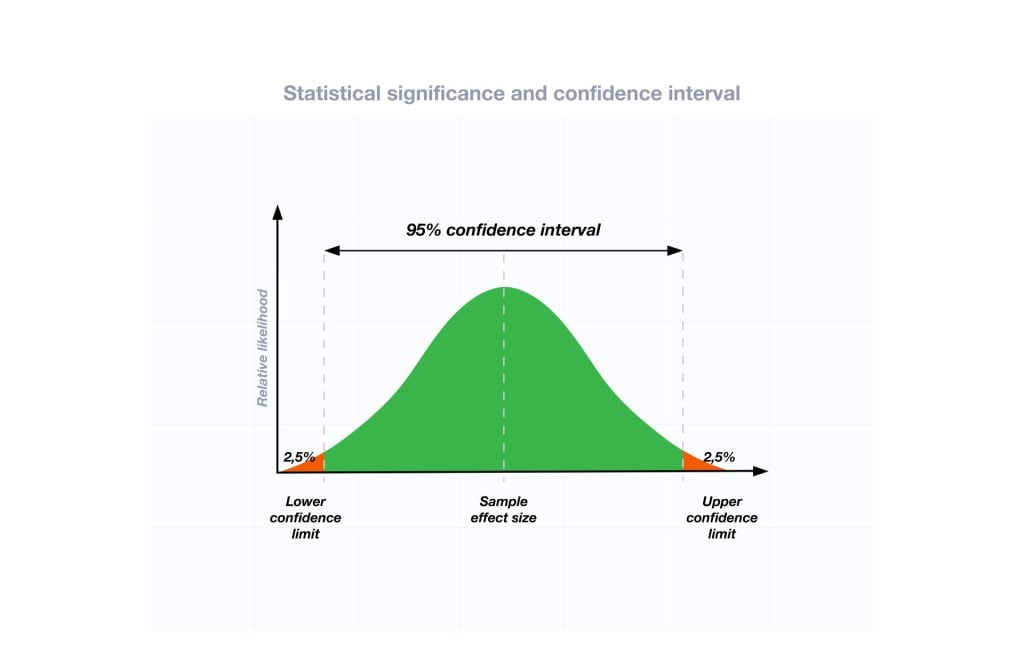
相应地,总体均值有5%的概率位于上下置信区间之外(如图所示,1.96 z分数两侧各有2.5%的异常值)。
为什么使用置信区间?
研究整个总体中的每个人几乎是不可能的,因此研究人员选择一个样本或总体的一个子群体。
这意味着研究人员只能估计总体的参数(即特征),估计范围是从一组给定的样本数据计算得出的。
因此,置信区间仅仅是一种衡量你的样本代表所研究总体程度的方法。
置信区间包含总体真实均值的概率称为置信水平。
你可以计算任何置信水平的置信区间,但最常用的值是95%。95%置信区间是一组值(上限和下限),你有95%的把握认为它包含了总体的真实均值。
如何计算
要计算置信区间,首先计算样本的均值和标准误差。
记住,你必须根据所选置信水平的z分数(见下表)计算置信区间的上界和下界。
| 置信水平 | Z分数 |
|---|---|
| 0.90 | 1.645 |
| 0.95 | 1.96 |
| 0.99 | 2.58 |
置信区间公式
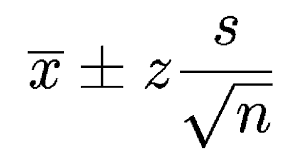
其中:
- X 是均值
- Z 是选定的Z值(95%时为1.96)
- s 是标准误差
- n 是样本量
对于下限值,将标准误差除以n的平方根,然后将此计算结果乘以z分数(95%时为1.96)。最后,从样本均值中减去此计算结果的值。
示例:
- X(均值)= 86
- Z = 1.960(上表95%时的值)
- s(标准误差)= 6.2
- n(样本量)= 46
下限值:86 – 1.960 × 6.2 √46 = 86 – 1.79 = 84.21
上限值:86 + 1.960 × 6.2 √46 = 86 + 1.79 = 87.79
因此,总体均值很可能在84.21和87.79之间。
总体均值与样本均值
我们如何确保总体均值与样本均值相似?
区间(上限和下限)越窄,我们的估计就越精确。
一般而言,随着样本量的增加,置信区间应该变得更窄。

因此,使用大样本可以比小样本更精确地估计总体均值。因此,从大样本计算出的置信区间相当窄。
如何报告
APA 6风格手册指出(第117页):
“报告置信区间时,使用格式95% CI [LL, UL],其中LL是置信区间的下限,UL是置信区间的上限。”
例如,可以报告95% CI [5.62, 8.31]。
置信区间也可以在表格中报告

进一步信息
常见问题
置信区间揭示了什么?
置信区间给出了我们认为某个数字(如平均数)可能位于的范围,基于我们的样本数据。置信水平(如95%)是我们对这个范围包含真实值的信心程度。
所以,如果我们有一个16岁青少年平均身高在5'4"到5'8"之间的95%置信区间,我们就是在说我们有95%的信心认为所有16岁青少年的真实平均身高在5'4"到5'8"之间。
这并不意味着所有身高都同样可能,只是说真实平均值可能落在这个范围内。这是一种展示我们估计不确定性的方法。
置信区间与标准差相同吗?
不,它们不同。标准差显示了一个组内各个测量值与平均值的差异程度。可以将其理解为学生分数与班级平均分的差异程度。
而置信区间则是我们非常确定(如95%确定)包含所有班级真实平均分数的范围,基于我们的班级。它是关于我们对估计真实平均值的信心程度,而不是关于个体差异。
盒形图显示置信区间吗?
标准盒形图显示中位数和四分位数范围,而不是置信区间。然而,一些增强的盒形图可以包括围绕中位数或均值的置信区间,通常用凹槽或误差线表示。
虽然这不是传统功能,但添加置信区间可以提供更多关于中心趋势估计可靠性的见解。
置信区间练习题
- 一名研究人员抽取了30名学生的测试成绩样本,平均分为85分,标准差为5分。测试成绩的95%置信区间是多少?
- 一项研究测量了50人的身高,发现平均身高为170厘米,标准差为10厘米。该人群身高的99%置信区间是多少?
- 在40个灯泡的样本中,平均寿命为5000小时,标准差为400小时。计算灯泡平均寿命的90%置信区间。
答案:
- 对于95%置信区间和样本量>30,我们通常使用z分数1.96。置信区间的公式为(均值 - (z (std_dev / sqrt(n))),均值 + (z (std_dev / sqrt(n)))。因此,置信区间为(85 - (1.96 (5 / sqrt(30))),85 + (1.96 (5 / sqrt(30))) = (83.21, 86.79)。
- 对于99%置信区间和样本量>30,我们通常使用z分数2.58。因此,置信区间为(170 - (2.58 (10 / sqrt(50))),170 + (2.58 (10 / sqrt(50))) = (167.35, 172.65)。
- 对于90%置信区间和样本量>30,我们通常使用z分数1.645。因此,置信区间为(5000 - (1.645 (400 / sqrt(40))),5000 + (1.645 (400 / sqrt(40))) = (4870.92, 5129.08)。
引用来源
本文翻译自以下网站:
simplypsychology.org
使用声明
本文仅供教育和参考用途。如需转载或引用,请注明出处和作者。
如果你有任何问题或建议,请随时联系微信公众号。