P-值和统计显著性：它是什么以及为什么重要

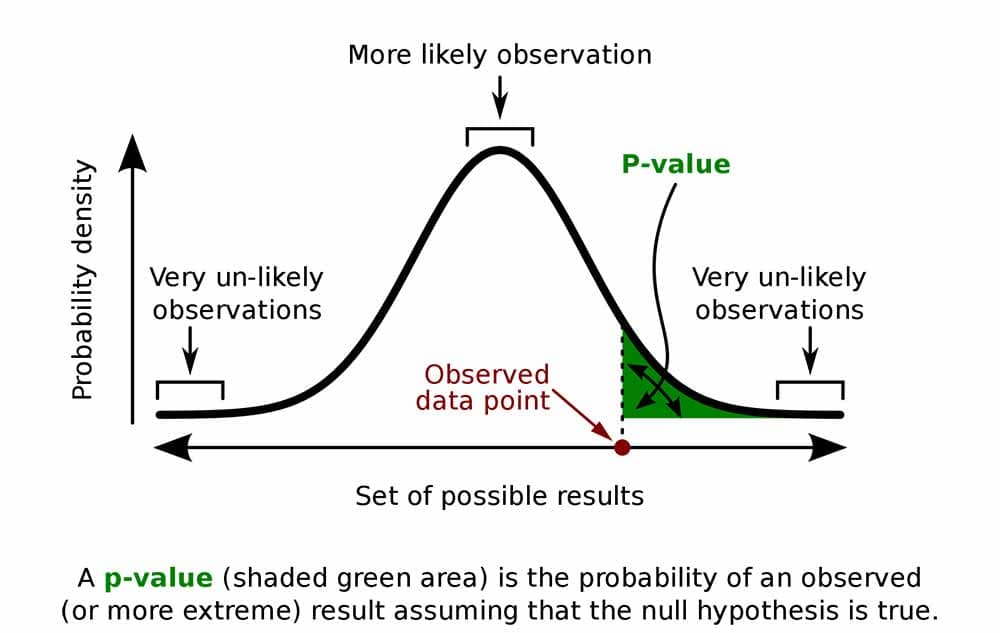
假设检验

当你进行统计检验时，P-值帮助你确定结果相对于零假设的重要性。

P-值告诉你什么

P-值，或概率值，是一个描述你的数据随机发生的可能性的数字（即零假设为真）。

统计显著性的水平通常用介于0到1之间的P-值表示。

P-值越小，结果由随机机会产生的可能性就越小，拒绝零假设的证据就越强。

记住，P-值并不能告诉你零假设是否为真或假。它只是告诉你如果零假设为真，观察到的数据（或更极端的数据）出现的可能性有多大。它是证据的一部分，而不是决定性的证明。

示例：检验统计量和P-值

假设你在进行一项研究，以确定一种新药与安慰剂相比是否对疼痛缓解有影响。

如果新药没有影响，你的检验统计量将接近零假设预测的值（药物组和安慰剂组之间没有差异），而得到的P-值将接近1。由于现实世界中可能存在变异，P-值可能不会精确地达到1。

相反，如果新药确实显著减轻了疼痛，你的检验统计量将远离零假设下的预期值，P-值将降低。

P-值永远不会达到零，因为即使是非常不可能的情况，观察到的结果也有可能是随机产生的。

P-值的解释

显著性水平（α）是一个设定的概率阈值（通常是0.05），而P-值是你根据研究或分析计算出的概率。

当P-值小于或等于你的显著性水平（通常≤0.05）时，结果具有统计显著性。

P-值小于或等于预设的显著性水平（通常为0.05或0.01）表明结果具有统计显著性，意味着观察到的数据提供了强烈的证据反对零假设。

这表明研究中的效应很可能代表了一种真实的关系，而不仅仅是随机机会。

例如，如果你设置α = 0.05，当你的P-值≤0.05时，你会拒绝零假设。

这表明有强烈的证据反对零假设，因为零假设正确的概率小于5%（结果是随机的）。

因此，我们拒绝零假设并接受备择假设。

示例：统计显著性

在分析新药与安慰剂在疼痛缓解效果上的差异后，计算出的P-值小于0.01，远低于预设的α值0.05。

因此，你得出结论，新药与安慰剂在疼痛缓解方面的差异具有统计显著性。

P-值为0.001意味着什么？

P-值为0.001远远超出了常用的0.05阈值，表明存在强烈的真实效应或差异，而不仅仅是随机变化。

具体来说，P-值为0.001意味着在零假设正确的情况下，获得至少与观察到的结果一样极端的结果的概率只有0.1%。

如此小的P-值提供了强烈的证据反对零假设，导致拒绝零假设而接受备择假设。

当P-值大于显著性水平（通常P > 0.05）时，结果不具有统计显著性，并表明支持零假设的强烈证据。

这意味着我们保留零假设并拒绝备择假设。你应该注意，你不能接受零假设；我们只能拒绝它或不拒绝它。

注意：当P-值高于你的显著性阈值时，并不意味着备择假设为真的概率为95%。

单尾检验

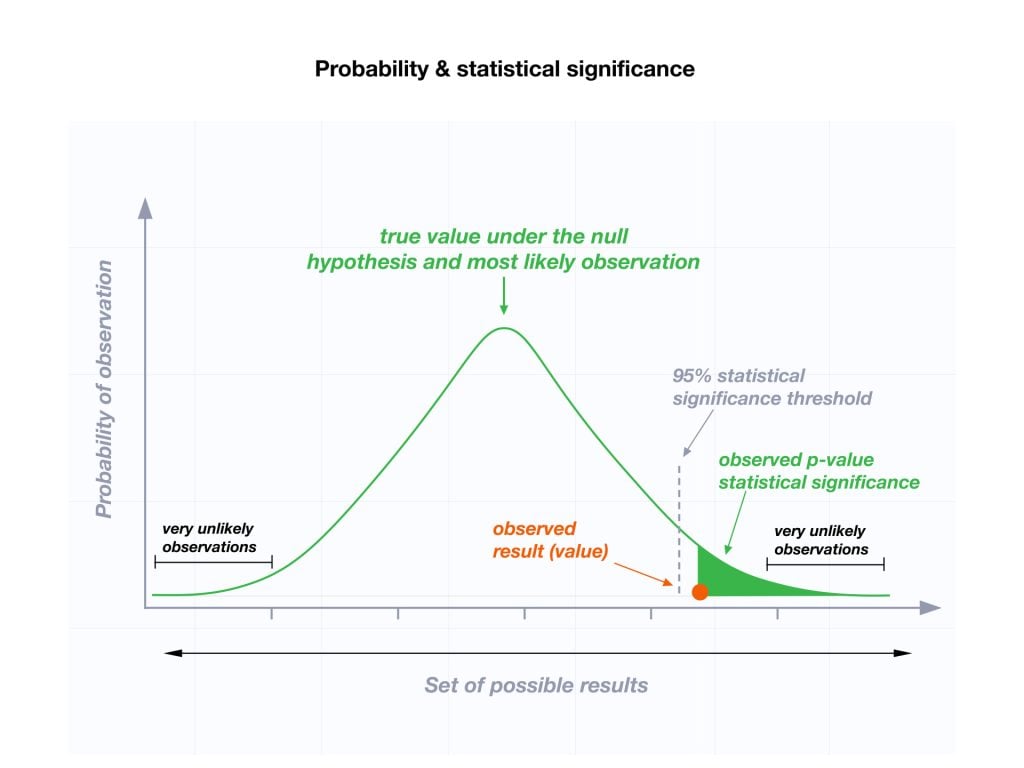
在正态分布中，显著性水平对应于曲线的尾部区域。在单尾检验中，整个显著性水平分配给分布的一个尾部。例如，如果你使用0.05（5%）的显著性水平，当你的数据点落在分布右端（对于右尾检验）或左端（对于左尾检验）的5%尾部时，你会拒绝零假设。在这个例子中，观察值具有统计显著性（P ≤ 0.05），因此拒绝零假设（H0），并接受备择假设（Ha）。

双尾检验

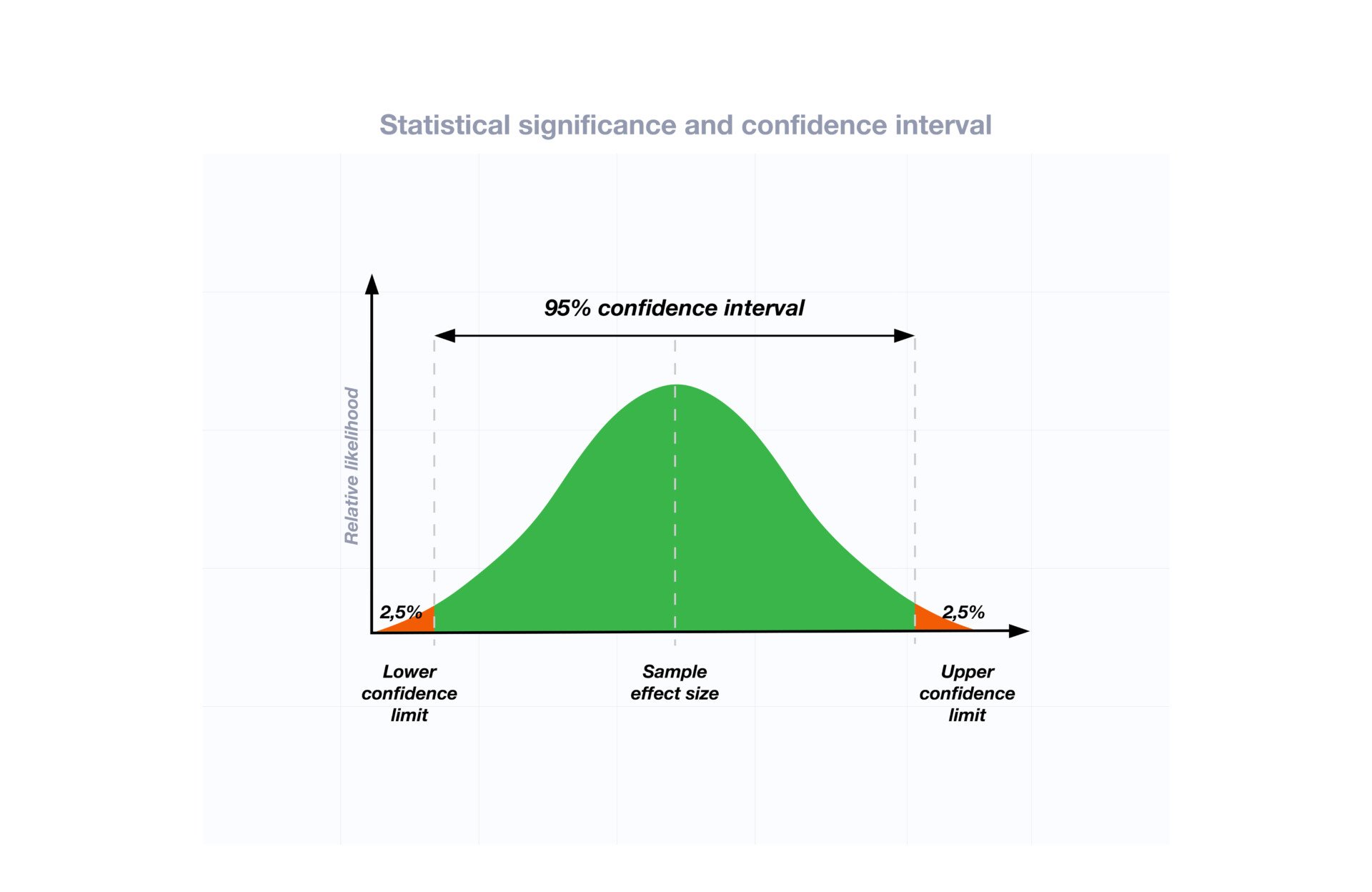
在正态分布中，显著性水平对应于曲线的尾部区域。在双尾检验中，你有两个各占曲线下面积2.5%的区域。任何落在这些极端区域的数据点都被认为在0.05水平上具有统计显著性，导致你拒绝零假设。

如何计算P-值？

大多数统计软件包如R、SPSS等会自动计算P-值。这是最简单和最常见的方法。

在线资源和表格可用于根据你的检验统计量和自由度来估算P-值。

这些表格帮助你理解在零假设下，期望看到你的检验统计量的频率。

理解统计检验：

不同的统计检验旨在回答特定的研究问题或假设。每个检验都有其自身的假设和特性。

例如，你可能会使用t检验来比较均值，使用卡方检验来处理分类数据，或使用相关性检验来测量变量之间关系的强度。

请注意，你在分析中包含的自变量数量会影响产生相同P-值所需的检验统计量的大小。

这一因素在比较不同分析的结果时尤为重要。

示例：选择统计检验

如果你正在比较两种不同药物在疼痛缓解方面的效果，使用两样本t检验是适合比较这两个组别的方法。然而，当你在考察三种或更多药物的影响时，采用方差分析（ANOVA)更为合适。

在这种情况下使用多重成对比较可能会导致人为降低p值，并高估药物组别之间差异的显著性。

如何报告

统计显著的结果不能证明研究假设是正确的（这暗示了100%的确定性）。

相反，我们可以陈述我们的结果“支持”或“提供证据支持”我们的研究假设（因为仍然存在一定的概率，即结果是由偶然产生的，而零假设是正确的——例如，小于5%）。

示例：报告结果

在我们比较新药与安慰剂的疼痛缓解效果时，观察到药物组的参与者经历了显著的疼痛减轻（M = 3.5; SD = 0.8），而安慰剂组的参与者则没有（M = 5.2; SD = 0.7），在疼痛量表上平均相差1.7分（t(98) = -9.36; p < 0.001）。

APA风格

美国心理学会（2010年）出版的APA风格手册第6版中关于报告p值的内容如下：

“在报告_p_值时，应报告精确的_p_值（例如，p = .031），保留两位或三位小数。但是，对于小于.001的_p_值，应报告为p < .001。报告_p_值的形式为p < .10, p < .05, p < .01等，在只有有限的关键值表格可用的时代是合适的。”（第114页）

注意事项：

不要在统计值_p_前使用0，因为它不可能等于1。换句话说，写p = .001而不是p = 0.001。
请注意斜体（_p_总是斜体）和空格（等号两侧）的问题。
p = .000（如SPSS等统计软件输出的）是不可能的，应写为p < .001。
显著性的反义词是“不显著”，而不是“微不足道”。

为什么_p_值不够？

较低的_p_值有时被解释为两个变量之间关系更强。

然而，统计显著性意味着零假设为真的可能性很小（小于5%）。

为了理解两组（对照组与实验组）之间的差异强度，研究人员需要计算效应量。

常见问题

何时拒绝零假设？

在统计假设检验中，当p值小于或等于你在进行测试之前设定的显著性水平（α）时，你会拒绝零假设。显著性水平是当零假设为真时拒绝它的概率。常用的显著性水平有0.01、0.05和0.10。

记住，拒绝零假设并不能证明备择假设；它只是表明根据观察到的数据，备择假设可能是合理的。

_p_值是在零假设为真的条件下得出的，但与备择假设的真假无关。

p值为0.05意味着什么？

如果p值小于或等于0.05（显著性水平），你会得出你的结果具有统计显著性的结论。这意味着证据足够强烈，可以拒绝零假设，转而支持备择假设。

所有低于0.05的p值都被认为是统计显著的吗？

不是所有低于0.05的p值都被认为是统计显著的。0.05这个阈值是常用的，但它只是一个惯例。统计显著性取决于诸如研究设计、样本大小和观察到的效果大小等因素。

p值低于0.05意味着有证据反对零假设，表明存在真实效应。然而，解释结果时考虑上下文和其他因素是非常重要的。

研究人员还查看效应量和置信区间，以确定发现的实际意义和可靠性。

样本大小如何影响p值的解释？

样本大小会影响p值的解释。更大的样本大小提供了更可靠和精确的总体估计，导致置信区间更窄。

较大的样本可以使即使是很小的组间差异或效应也变得统计显著，从而产生更低的p值。相反，较小的样本可能没有足够的统计功效来检测较小的效应，从而导致更高的p值。

因此，较大的样本增加了在存在真实效应时找到统计显著结果的机会，使结果更加可信和稳健。

非显著的p值是否意味着数据中没有效应或差异？

非显著的p值并不一定意味着数据中没有效应或差异。它意味着观察到的数据不足以拒绝零假设。

仍可能存在真实的效应或差异，但它可能比研究能够检测到的要小或变化更大。

其他因素如样本大小、研究设计和测量精度也会影响p值。解释研究结果时，不应仅依赖p值，而应考虑整个证据体系。

p值可以正好为零吗？

虽然p值可以非常小，但技术上它不可能是绝对零。当p值报告为p = 0.000时，实际的p值太小，软件无法显示。这通常被解释为反对零假设的强证据。对于小于0.001的p值，应报告为p < .001。

进一步信息

参考文献

Bland, J. M., & Altman, D. G. (1994). 单侧和双侧显著性检验：作者回复。BMJ: British Medical Journal, 309(6958), 874.

Goodman, S. N., & Royall, R. (1988). 证据与科学研究。American Journal of Public Health, 78(12), 1568-1574.

Goodman, S. (2008, July). 十二个p值误解. In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). 令人困惑的P值。Epidemiology (Cambridge, Mass.), 9(1), 7-8.

引用来源

本文翻译自以下网站：

simplypsychology.org

使用声明

本文仅供教育和参考用途。如需转载或引用，请注明出处和作者。

如果你有任何问题或建议，请随时联系微信公众号。

聚观点

聚观点